最新更新于: 2024年5月24日上午11点17分
数学分析第一周,讲了多元函数 关于 R i e m a n n Riemann R i e m a n n D a r b o u x Darboux D a r b o u x L e b e s g u e Lebesgue L e b e s g u e
多元函数的 R i e m a n n Riemann R i e m a n n R i e m a n n Riemann R i e m a n n R i e m a n n Riemann R i e m a n n I I I I I I f f f Q Q Q R i e m a n n Riemann R i e m a n n
于是先定义下前置芝士:
闭方体 :Q = ∏ i = 1 n [ a i , b i ] , − ∞ < a i < b i < + ∞ \displaystyle Q=\prod_{i=1}^n[a_i,b_i],\ -\infty < a_i < b_i < +\infty Q = i = 1 ∏ n [ a i , b i ] , − ∞ < a i < b i < + ∞
直径 :diam Q = ∑ i ( b i − a i ) 2 \text{diam}Q = \sqrt{\sum_i(b_i-a_i)^2} diam Q = ∑ i ( b i − a i ) 2
“体积” (在三维的时候叫体积,二维叫面积):V ( Q ) = ∏ i ∣ b i − a i ∣ V(Q)=\prod_i\mid b_i-a_i\mid V ( Q ) = ∏ i ∣ b i − a i ∣
分划 :
先定义第 i i i [ a i , b i ] [a_i,b_i] [ a i , b i ] a i = c i 0 < c i 1 < ⋯ < c i N i = b i a_i=c_i^0 < c_i^1 < \cdots < c_i^{N_i} = b_i a i = c i 0 < c i 1 < ⋯ < c i N i = b i ( 1 ⩽ i ⩽ n ) (1\leqslant i\leqslant n) ( 1 ⩽ i ⩽ n )
n n n Q Q Q π = { ∏ i = 1 n [ c i j i − 1 , c i j i ] : 1 ⩽ j i ⩽ N i , 1 ⩽ i ⩽ n } \displaystyle\pi = \{\prod_{i=1}^n[c_i^{j_i-1}, c_i^{j_i}]:1\leqslant j_i\leqslant N_i, 1\leqslant i\leqslant n\} π = { i = 1 ∏ n [ c i j i − 1 , c i j i ] : 1 ⩽ j i ⩽ N i , 1 ⩽ i ⩽ n }
分划程度 :Δ π = max q ∈ π diam ( q ) \Delta\pi=\max\limits_{q\in\pi}\text{diam}(q) Δ π = q ∈ π max diam ( q )
分划的细分 :对于 Q Q Q π 1 , π 2 \pi_1, \pi_2 π 1 , π 2 ∀ q ∈ π 2 , ∃ p ∈ π 1 \forall q\in\pi_2, \exists p\in\pi_1 ∀ q ∈ π 2 , ∃ p ∈ π 1 q ⊂ p q\subset p q ⊂ p π 2 \pi_2 π 2 π 1 \pi_1 π 1 π 2 ⩾ π 1 \pi_2\geqslant \pi_1 π 2 ⩾ π 1
立方体的中心 :若 q = ∏ i [ a i , b i ] \displaystyle q=\prod_{i}[a_i,b_i] q = i ∏ [ a i , b i ] q q q c q = ( a i + b i 2 ) i = 1 n c_q=\left(\frac{a_i+b_i}{2}\right)^n_{i=1} c q = ( 2 a i + b i ) i = 1 n
以中心放缩 :设 r > 0 r > 0 r > 0 q q q r r r r q : = { r ( x − c ) + c : x ∈ q } rq:=\{r(x-c)+c:x\in q\} r q : = { r ( x − c ) + c : x ∈ q }
Q ⊂ R n Q\subset \mathbb R^n Q ⊂ R n f : Q → R f:Q\rightarrow \mathbb{R} f : Q → R π \pi π Q Q Q
S = ∑ q ∈ π f ( ξ q ) V ( q ) S=\sum_{q\in\pi}f(\xi_q)V(q)
S = q ∈ π ∑ f ( ξ q ) V ( q )
其中 ξ q ∈ q \xi_q\in q ξ q ∈ q S S S f f f π \pi π R i e m a n n Riemann R i e m a n n
设 I ∈ R I\in\mathbb R I ∈ R ∀ ε > 0 , ∃ δ > 0 \forall \varepsilon > 0, \exists \delta > 0 ∀ ε > 0 , ∃ δ > 0 Δ π ⩽ δ \Delta\pi\leqslant \delta Δ π ⩽ δ ∣ S − I ∣ ⩽ ε \mid S-I\mid \leqslant \varepsilon ∣ S − I ∣ ⩽ ε
则称 lim Δ π → 0 S \lim\limits_{\Delta\pi\rightarrow 0} S Δ π → 0 lim S lim Δ π → 0 S = I \lim\limits_{\Delta\pi\rightarrow 0}S=I Δ π → 0 lim S = I
如果 lim Δ π → 0 S \lim\limits_{\Delta\pi\rightarrow 0}S Δ π → 0 lim S f R i e m a n n f\ Riemann f R i e m a n n ∫ Q f ( x ) d x = lim Δ π → 0 S \int_Q f(x)\,dx = \lim\limits_{\Delta\pi\rightarrow 0}S ∫ Q f ( x ) d x = Δ π → 0 lim S ∫ Q f \int_Q f ∫ Q f
注 :这里的 x x x n n n x ⃗ \vec{x} x x x x n n n
不难发现,常值函数 f ( x ) = C f(x)=C f ( x ) = C Q Q Q R i e m a n n Riemann R i e m a n n ∫ Q f = C ⋅ V ( Q ) \int_Q f=C\cdot V(Q) ∫ Q f = C ⋅ V ( Q ) C = 1 C=1 C = 1 Q Q Q V ( Q ) V(Q) V ( Q )
如果 f R i e m a n n f\ Riemann f R i e m a n n f f f
思路 :先随便取一个分划 π \pi π Q Q Q π \pi π R i e m a n n Riemann R i e m a n n
证明 :
有 R i e m a n n Riemann R i e m a n n ∣ ∑ q ∈ π f ( ξ q ) V ( q ) − I ∣ ⩽ 1 \displaystyle \left|\sum_{q\in\pi}f(\xi_q)V(q)-I\right|\leqslant 1 ∣ ∣ ∣ ∣ ∣ ∣ q ∈ π ∑ f ( ξ q ) V ( q ) − I ∣ ∣ ∣ ∣ ∣ ∣ ⩽ 1
对于 ∀ x ∈ Q \forall x\in Q ∀ x ∈ Q ∃ p ∈ π \exists p\in\pi ∃ p ∈ π x ∈ p x\in p x ∈ p c q c_q c q q q q
∣ f ( x ) V ( p ) + ∑ q ∈ π , q ≠ p f ( c q ) V ( q ) − I ∣ ⩽ 1 ⇒ ∣ f ( x ) ∣ ⋅ V ( p ) ⩽ ∑ q ∈ π ∣ f ( c q ) ∣ V ( q ) + ∣ I ∣ + 1 , 令 m = min q ∈ π V ( q ) ⇒ ∣ f ( x ) ∣ ⩽ ( ∑ q ∈ π ∣ f ( c q ) ∣ V ( q ) + ∣ I ∣ + 1 ) / m \begin{aligned}
&\left|f(x)V(p)+\sum_{q\in\pi,q\neq p}f(c_q)V(q)-I\right|\leqslant 1\\
\Rightarrow&|f(x)|\cdot V(p)\leqslant \sum_{q\in\pi}|f(c_q)|V(q)+|I|+1,\ \text{令} m=\min\limits_{q\in\pi}V(q)\\
\Rightarrow&|f(x)|\leqslant \left(\sum_{q\in\pi}|f(c_q)|V(q)+|I|+1\right)/m
\end{aligned}
⇒ ⇒ ∣ ∣ ∣ ∣ ∣ ∣ ∣ f ( x ) V ( p ) + q ∈ π , q = p ∑ f ( c q ) V ( q ) − I ∣ ∣ ∣ ∣ ∣ ∣ ∣ ⩽ 1 ∣ f ( x ) ∣ ⋅ V ( p ) ⩽ q ∈ π ∑ ∣ f ( c q ) ∣ V ( q ) + ∣ I ∣ + 1 , 令 m = q ∈ π min V ( q ) ∣ f ( x ) ∣ ⩽ ( q ∈ π ∑ ∣ f ( c q ) ∣ V ( q ) + ∣ I ∣ + 1 ) / m
右式中和左侧的 x x x f f f Q Q Q
(引入中心点 c q c_q c q π \pi π
QED
设 f : Q → R f:Q\rightarrow \mathbb{R} f : Q → R A ⊂ Q A\subset Q A ⊂ Q
m A = inf a ∈ A f ( a ) = inf A f m_A=\inf\limits_{a\in A}f(a)=\inf\limits_A f m A = a ∈ A inf f ( a ) = A inf f M A = sup a ∈ A f ( a ) = sup A f M_A=\sup\limits_{a\in A}f(a)=\sup\limits_A f M A = a ∈ A sup f ( a ) = A sup f w A = M A − m A w_A=M_A-m_A w A = M A − m A f f f A A A 振幅
设 π \pi π Q Q Q
Darboux下和:S ‾ ( π ) = ∑ q ∈ π m q V ( q ) \underline{S}(\pi) = \sum\limits_{q\in\pi}m_qV(q) S ( π ) = q ∈ π ∑ m q V ( q )
Darboux上和:S ‾ ( π ) = ∑ q ∈ π M q V ( q ) \overline{S}(\pi) = \sum\limits_{q\in\pi}M_qV(q) S ( π ) = q ∈ π ∑ M q V ( q )
设 Q Q Q π 1 , π 2 \pi_1,\pi_2 π 1 , π 2 π 2 ⩾ π 1 \pi_2\geqslant \pi_1 π 2 ⩾ π 1 S ‾ ( π 2 ) ⩽ S ‾ ( π 1 ) , S ‾ ( π 2 ) ⩾ S ‾ ( π 1 ) \overline{S}(\pi_2)\leqslant \overline{S}(\pi_1), \underline{S}(\pi_2)\geqslant \underline{S}(\pi_1) S ( π 2 ) ⩽ S ( π 1 ) , S ( π 2 ) ⩾ S ( π 1 )
思路 :通过细分的性质,将属于同一个 p p p q q q m A m_A m A
对于任意两个 Q Q Q π 1 , π 2 \pi_1,\pi_2 π 1 , π 2 S ‾ ( π 1 ) ⩽ S ‾ ( π 2 ) \underline{S}(\pi_1)\leqslant\overline{S}(\pi_2) S ( π 1 ) ⩽ S ( π 2 )
思路 :引入一个 π \pi π π ⩽ π 1 \pi\leqslant \pi_1 π ⩽ π 1 π ⩽ π 2 \pi\leqslant\pi_2 π ⩽ π 2
对于任意的 Q Q Q π \pi π
Darboux下积分:∫ ‾ Q f = sup π S ‾ ( π ) = sup π ( ∑ q ∈ π ( inf q f ) V ( q ) ) \underline{\int}_Q f = \sup\limits_\pi \underline{S}(\pi) = \sup\limits_\pi\left(\sum\limits_{q\in\pi}\left(\inf\limits_qf\right)V(q)\right) ∫ Q f = π sup S ( π ) = π sup ( q ∈ π ∑ ( q inf f ) V ( q ) )
Darboux上积分:∫ ‾ Q f = inf π S ‾ ( π ) = inf π ( ∑ q ∈ π ( sup q f ) V ( q ) ) \overline{\int}_Q f = \inf\limits_\pi \overline{S}(\pi) = \inf\limits_\pi\left(\sum\limits_{q\in\pi}\left(\sup\limits_qf\right)V(q)\right) ∫ Q f = π inf S ( π ) = π inf ( q ∈ π ∑ ( q sup f ) V ( q ) )
则有:∫ ‾ Q f ⩽ ∫ ‾ Q f \underline{\int}_Qf\leqslant\overline{\int}_Qf ∫ Q f ⩽ ∫ Q f
若 ∫ ‾ Q f = ∫ ‾ Q f \underline{\int}_Qf = \overline{\int}_Qf ∫ Q f = ∫ Q f f D a r b o u x f\ Darboux f D a r b o u x ∫ ‾ Q f \underline{\int}_Qf ∫ Q f f f f D a r b o u x Darboux D a r b o u x
⟺ \iff ⟺ 设 Q ⊂ R n Q\subset \mathbb{R}^n Q ⊂ R n f : Q → R f:Q\rightarrow \mathbb{R} f : Q → R
f R i e m a n n f\ Riemann f R i e m a n n
f D a r b o u x f\ Darboux f D a r b o u x
∀ ε > 0 \forall \varepsilon > 0 ∀ ε > 0 Q Q Q π \pi π ∑ q ∈ π w q V ( q ) ⩽ ε \sum\limits_{q\in\pi}w_qV(q)\leqslant\varepsilon q ∈ π ∑ w q V ( q ) ⩽ ε
∀ ε > 0 , ∃ δ > 0 \forall \varepsilon > 0, \exists \delta > 0 ∀ ε > 0 , ∃ δ > 0 Q Q Q Δ π ⩽ δ \Delta\pi \leqslant \delta Δ π ⩽ δ π \pi π ∑ q ∈ π w q V ( q ) ⩽ ε \sum\limits_{q\in\pi}w_qV(q)\leqslant \varepsilon q ∈ π ∑ w q V ( q ) ⩽ ε
思路 :分别考虑四个证明:
① ⇒ ② : ①\Rightarrow ②: ① ⇒ ② : R i e m a n n Riemann R i e m a n n ε \varepsilon ε D a r b o u x Darboux D a r b o u x ε \varepsilon ε
② ⇒ ③ : ②\Rightarrow ③: ② ⇒ ③ : D a r b o u x Darboux D a r b o u x ε \varepsilon ε ε \varepsilon ε
④ ⇒ ① : ④\Rightarrow ①: ④ ⇒ ① : R i e m a n n Riemann R i e m a n n D a r b o u x Darboux D a r b o u x R i e m a n n Riemann R i e m a n n R i e m a n n Riemann R i e m a n n
③ ⇒ ④ : ③\Rightarrow ④: ③ ⇒ ④ :
引理1 :设 K ⊂ R n K\subset \mathbb{R}^n K ⊂ R n Ω ⫋ R n \Omega \subsetneqq \mathbb{R}^n Ω ⫋ R n K ⊂ Ω K\subset \Omega K ⊂ Ω
dist ( K , ∂ Ω ) : = inf x ∈ K , y ∈ ∂ Ω ∣ x − y ∣ > 0 \text{dist}(K, \partial \Omega):=\inf\limits_{x\in K, y\in\partial\Omega} |x-y| > 0
dist ( K , ∂ Ω ) : = x ∈ K , y ∈ ∂ Ω inf ∣ x − y ∣ > 0
思路 :对紧集 K K K 有限覆盖定理 ,有限覆盖定理可以将一个紧集(可能有无限个元素)拆分成有限个“点”(很小的开集)组成,于是考虑每个“点”的一个半径为 r i r_i r i Ω \Omega Ω
dist ( K , ∂ Ω ) > min i ( r i ) > 0 \text{dist}(K, \partial \Omega) > \min\limits_{i}(r_i) > 0
dist ( K , ∂ Ω ) > i min ( r i ) > 0
引理2 :设 P i , ( 1 ⩽ i ⩽ m ) P_i, (1\leqslant i\leqslant m) P i , ( 1 ⩽ i ⩽ m ) Q j , ( 1 ⩽ j ⩽ l ) Q_j, (1\leqslant j\leqslant l) Q j , ( 1 ⩽ j ⩽ l ) Q j ∘ Q_j^{\circ} Q j ∘
⋃ j Q j ⊂ ⋃ i P i \bigcup_{j}Q_j\subset\bigcup_{i}P_i
j ⋃ Q j ⊂ i ⋃ P i
则有
∑ i V ( P i ) ⩾ ∑ j V ( Q j ) \sum_iV(P_i)\geqslant \sum_jV(Q_j)
i ∑ V ( P i ) ⩾ j ∑ V ( Q j )
思路 :如果 ⋃ j Q j = ⋃ i P i \bigcup\limits_{j}Q_j=\bigcup\limits_{i}P_i j ⋃ Q j = i ⋃ P i { Q j } \{Q_j\} { Q j } ⋃ i P i \bigcup\limits_{i}P_i i ⋃ P i ⋃ j Q j ⫋ ⋃ i P i \bigcup_{j}Q_j\subsetneqq\bigcup_{i}P_i ⋃ j Q j ⫋ ⋃ i P i Q Q Q P P P
原命题证明的大致思路 :随便给出一个满足条件 3 3 3 ( 1 − ε ) (1-\varepsilon) ( 1 − ε ) Δ π ⩽ min p dist ( ( 1 − ε ) p , ∂ p ) / 2 \Delta\pi\leqslant \min\limits_p \text{dist}((1-\varepsilon)p, \partial p)/2 Δ π ⩽ p min dist ( ( 1 − ε ) p , ∂ p ) / 2 4 4 4
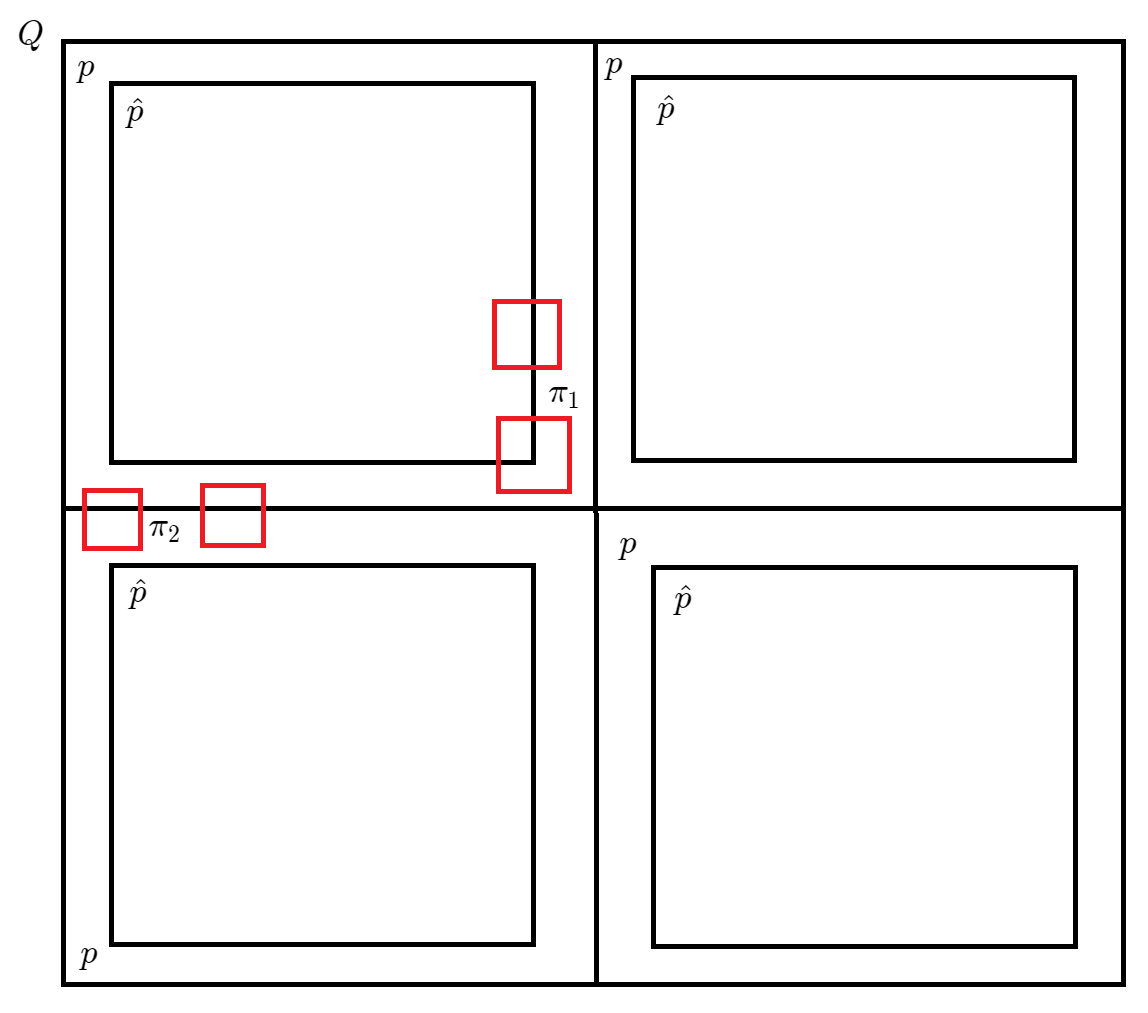
③ ⇒ ④ ③\Rightarrow ④ ③ ⇒ ④ 证明 :设 0 < ε < 1 0 < \varepsilon < 1 0 < ε < 1 Q Q Q α \alpha α ∑ p ∈ α w p V ( p ) ⩽ ε \sum\limits_{p\in\alpha}w_pV(p)\leqslant\varepsilon p ∈ α ∑ w p V ( p ) ⩽ ε
设 p ∈ α p\in\alpha p ∈ α p ^ = ( 1 − ε ) p \hat{p} = (1- \varepsilon) p p ^ = ( 1 − ε ) p p p p ( 1 − ε ) (1-\varepsilon) ( 1 − ε ) 前置定义 ),
则 p ^ ⊂ p ∘ \hat{p}\subset p^\circ p ^ ⊂ p ∘ 引理1 知:dist ( p ^ , ∂ p ) > 0 \text{dist}(\hat{p}, \partial p) > 0 dist ( p ^ , ∂ p ) > 0
取 δ = min p ∈ α dist ( p ^ , ∂ p ) / 2 \delta = \min\limits_{p\in\alpha} \text{dist}(\hat{p}, \partial p) / 2 δ = p ∈ α min dist ( p ^ , ∂ p ) / 2
设 π \pi π Δ π ⩽ δ \Delta\pi\leqslant \delta Δ π ⩽ δ ∑ q ∈ π w q V ( q ) ⩽ C ⋅ ε \sum\limits_{q\in\pi} w_qV(q)\leqslant C\cdot \varepsilon q ∈ π ∑ w q V ( q ) ⩽ C ⋅ ε π \pi π p ^ \hat{p} p ^ π 1 \pi_1 π 1 π 2 \pi_2 π 2 π 1 , π 2 \pi_1,\pi_2 π 1 , π 2 ε \varepsilon ε
π 1 = { q ∈ π : ∃ p 0 ∈ α , q ∩ p 0 ^ ≠ ∅ } \pi_1 = \{q\in\pi:\exists p_0\in \alpha, q\cap\hat{p_0}\neq \varnothing\} π 1 = { q ∈ π : ∃ p 0 ∈ α , q ∩ p 0 ^ = ∅ }
π 2 = { q ∈ π : ∀ p ∈ α , q ∩ p ^ = ∅ } \pi_2 = \{q\in\pi:\forall p\in\alpha, q\cap\hat{p} = \varnothing\} π 2 = { q ∈ π : ∀ p ∈ α , q ∩ p ^ = ∅ }
则 π = π 1 + π 2 \pi = \pi_1+\pi_2 π = π 1 + π 2 ∑ q ∈ π w q V ( q ) = ∑ q ∈ π 1 w q V ( q ) + ∑ q ∈ π 2 w q V ( q ) \displaystyle \sum_{q\in\pi}w_qV(q)=\sum_{q\in\pi_1}w_qV(q)+\sum_{q\in\pi_2}w_qV(q) q ∈ π ∑ w q V ( q ) = q ∈ π 1 ∑ w q V ( q ) + q ∈ π 2 ∑ w q V ( q )
分为两部分解决:
π 1 \pi_1 π 1 π 1 \pi_1 π 1 p p p Δ π \Delta\pi Δ π
设 q ∈ π 1 , ∃ p ∈ α q\in\pi_1, \exists p\in\alpha q ∈ π 1 , ∃ p ∈ α p ^ ∩ q ≠ ∅ \hat{p}\cap q\neq \varnothing p ^ ∩ q = ∅ dist ( p ^ , ∂ p ) ⩾ 2 δ \text{dist}(\hat{p}, \partial p)\geqslant 2\delta dist ( p ^ , ∂ p ) ⩾ 2 δ diam q ⩽ δ \text{diam } q\leqslant \delta diam q ⩽ δ q ⊂ p q\subset p q ⊂ p
对 π 1 \pi_1 π 1 π 1 , p = { q ∈ π 1 : q ⊂ p } , p ∈ α \pi_{1, p} = \{q\in\pi_1: q\subset p\}, p\in\alpha π 1 , p = { q ∈ π 1 : q ⊂ p } , p ∈ α
当 p 1 ≠ p 2 p_1\neq p_2 p 1 = p 2 π 1 , p 1 ∩ π 1 , p 2 = ∅ \pi_{1,p_1}\cap\pi_{1,p_2} = \varnothing π 1 , p 1 ∩ π 1 , p 2 = ∅ π 1 = ∑ p ∈ α π 1 , p \pi_1=\sum\limits_{p\in\alpha}\pi_{1, p} π 1 = p ∈ α ∑ π 1 , p ∑ \sum ∑
于是有(第二个不等号处使用了引理2 ):
∑ q ∈ π 1 w q V ( q ) = ∑ p ∈ α ∑ q ∈ π 1 , p w q V ( q ) ⩽ ∑ p ∈ α w p ∑ q ∈ π 1 , p V ( q ) ⩽ ∑ p ∈ α w p V ( p ) ⩽ ε \sum_{q\in\pi_1}w_qV(q)=\sum_{p\in\alpha}\sum_{q\in{\pi_{1, p}}} w_qV(q)\leqslant \sum_{p\in\alpha}w_p\sum_{q\in\pi_{1,p}}V(q)\leqslant \sum_{p\in\alpha}w_pV(p)\leqslant \varepsilon
q ∈ π 1 ∑ w q V ( q ) = p ∈ α ∑ q ∈ π 1 , p ∑ w q V ( q ) ⩽ p ∈ α ∑ w p q ∈ π 1 , p ∑ V ( q ) ⩽ p ∈ α ∑ w p V ( p ) ⩽ ε
下面证明 π 2 \pi_2 π 2
f f f ∣ f ∣ ⩽ M |f|\leqslant M ∣ f ∣ ⩽ M f f f M M M ∑ q ∈ π 2 w q V ( q ) ⩽ 2 M ∑ q ∈ π 2 V ( q ) \displaystyle \sum_{q\in\pi_2}w_qV(q)\leqslant 2M\sum_{q\in\pi_2}V(q) q ∈ π 2 ∑ w q V ( q ) ⩽ 2 M q ∈ π 2 ∑ V ( q )
由于 V ( Q ) = ∑ q ∈ π 1 V ( q ) + ∑ q ∈ π 2 V ( q ) , ⋃ p ∈ α p ^ ⊂ ⋃ q ∈ π 1 q \displaystyle V(Q) = \sum_{q\in\pi_1} V(q) +\sum_{q\in\pi_2} V(q), \bigcup_{p\in\alpha} \hat{p}\subset\bigcup_{q\in\pi_1}q V ( Q ) = q ∈ π 1 ∑ V ( q ) + q ∈ π 2 ∑ V ( q ) , p ∈ α ⋃ p ^ ⊂ q ∈ π 1 ⋃ q
则 ∑ q ∈ π 1 V ( q ) ⩾ ∑ p ∈ α V ( p ^ ) = ( 1 − ε ) n ⋅ V ( Q ) \displaystyle \sum_{q\in\pi_1}V(q)\geqslant \sum_{p\in\alpha}V(\hat{p}) = (1-\varepsilon)^n\cdot V(Q) q ∈ π 1 ∑ V ( q ) ⩾ p ∈ α ∑ V ( p ^ ) = ( 1 − ε ) n ⋅ V ( Q )
故(第二个不等号使用Bernoulli 不等式
∑ q ∈ π 2 w q V ( q ) ⩽ 2 M ( 1 − ( 1 − ε ) n ) V ( Q ) ⩽ 2 M n V ( Q ) ε ⩽ C ⋅ ε \sum_{q\in\pi_2}w_qV(q)\leqslant 2M(1-(1-\varepsilon)^n)V(Q)\leqslant 2MnV(Q)\varepsilon\leqslant C\cdot \varepsilon
q ∈ π 2 ∑ w q V ( q ) ⩽ 2 M ( 1 − ( 1 − ε ) n ) V ( Q ) ⩽ 2 M n V ( Q ) ε ⩽ C ⋅ ε
综上:∑ q ∈ π w q V ( q ) ⩽ ( C + 1 ) ε \sum\limits_{q\in\pi}w_qV(q)\leqslant (C+1)\varepsilon q ∈ π ∑ w q V ( q ) ⩽ ( C + 1 ) ε
QED
思考: 看似 ③ ③ ③ ④ ④ ④ ③ ③ ③ ④ ④ ④ δ \delta δ ④ ④ ④ π \pi π ③ ③ ③
定义开方体 : Q = ∏ i = 1 n ( a i , b i ) \displaystyle Q=\prod_{i=1}^n(a_i, b_i) Q = i = 1 ∏ n ( a i , b i ) V ( Q ) = ∏ i = 1 n ( b i − a i ) \displaystyle V(Q)=\prod\limits_{i=1}^n(b_i-a_i) V ( Q ) = i = 1 ∏ n ( b i − a i )
设 A ⊂ R n A\subset \mathbb{R}^n A ⊂ R n
m ∗ ( A ) = inf { ∑ j ∈ J V ( Q j ) : J 为可数集 , Q j 为开方体 , A ⊂ ⋃ j ∈ J Q j } m^*(A) = \inf\left\{\sum_{j\in J} V(Q_j): J\text{为可数集}, Q_j\text{为开方体}, A\subset\bigcup_{j\in J} Q_j\right\}
m ∗ ( A ) = inf ⎩ ⎪ ⎨ ⎪ ⎧ j ∈ J ∑ V ( Q j ) : J 为可数集 , Q j 为开方体 , A ⊂ j ∈ J ⋃ Q j ⎭ ⎪ ⎬ ⎪ ⎫
称为 A A A n n n L e b e s g u e Lebesgue L e b e s g u e A A A
如果 A ⊂ R n , m ∗ ( A ) = 0 A\subset\mathbb{R}^n, m^*(A)=0 A ⊂ R n , m ∗ ( A ) = 0 A A A L e b e s g u e Lebesgue L e b e s g u e
m ∗ ( ∅ ) = 0 , 0 ⩽ m ∗ ( A ) ⩽ + ∞ m^*(\varnothing) = 0, 0\leqslant m^*(A)\leqslant +\infty m ∗ ( ∅ ) = 0 , 0 ⩽ m ∗ ( A ) ⩽ + ∞
若 A , A k ⊂ R n A, A_k\subset \mathbb{R}^n A , A k ⊂ R n A ⊂ ⋃ k = 1 ∞ A k A\subset\bigcup\limits_{k=1}^\infty A_k A ⊂ k = 1 ⋃ ∞ A k m ∗ ( A ) ⩽ ∑ k m ∗ ( A k ) m^*(A)\leqslant \sum\limits_km^*(A_k) m ∗ ( A ) ⩽ k ∑ m ∗ ( A k )
若 A ⊂ B ⊂ R n A\subset B\subset \mathbb{R}^n A ⊂ B ⊂ R n m ∗ ( A ) ⩽ m ∗ ( B ) m^*(A)\leqslant m^*(B) m ∗ ( A ) ⩽ m ∗ ( B )
若 A k ⊂ R n A_k\subset\mathbb{R}^n A k ⊂ R n m ∗ ( ⋃ k = 1 ∞ A k ) ⩽ ∑ k = 1 ∞ m ∗ ( A k ) m^*(\bigcup\limits_{k=1}^\infty A_k)\leqslant \sum\limits_{k=1}^\infty m^*(A_k) m ∗ ( k = 1 ⋃ ∞ A k ) ⩽ k = 1 ∑ ∞ m ∗ ( A k )
设 A ⊂ R n , r > 0 A\subset \mathbb{R}^n, r > 0 A ⊂ R n , r > 0 A + b : = { x + b : x ∈ A } A+b:=\{x+b:x\in A\} A + b : = { x + b : x ∈ A } m ∗ ( A + b ) = m ∗ ( A ) m^*(A+b)=m^*(A) m ∗ ( A + b ) = m ∗ ( A )
设 A ⊂ R n , r > 0 A\subset \mathbb{R}^n, r>0 A ⊂ R n , r > 0 r A : = { r x : x ∈ A } rA:=\{rx:x\in A\} r A : = { r x : x ∈ A } m ∗ ( r A ) = r n m ∗ ( A ) m^*(rA)=r^nm^*(A) m ∗ ( r A ) = r n m ∗ ( A )
若 Q ⊂ R n Q\subset \mathbb{R}^n Q ⊂ R n m ∗ ( Q ) = V ( Q ) = m ∗ ( Q ‾ ) m^*(Q) = V(Q) = m^*(\overline{Q}) m ∗ ( Q ) = V ( Q ) = m ∗ ( Q )
例1 :m ∗ ( { a } ) = 0 m^*(\{a\}) = 0 m ∗ ( { a } ) = 0
例2 :m ∗ ( { a 1 , a 2 , … } ) ⩽ ∑ i m ∗ ( { a i } ) = 0 m^*(\{a_1,a_2,\ldots\})\leqslant \sum\limits_i m^*(\{a_i\}) = 0 m ∗ ( { a 1 , a 2 , … } ) ⩽ i ∑ m ∗ ( { a i } ) = 0 a i a_i a i 可数个 即可)
设 K ⊂ R n − 1 K\subset \mathbb{R}^{n-1} K ⊂ R n − 1 f ∈ C ( K ) f\in C(K) f ∈ C ( K ) C ( K ) C(K) C ( K ) K K K F = graph f = { ( x , f ( x ) ) : x ∈ K } F=\text{graph } f=\{(x, f(x)):x\in K\} F = graph f = { ( x , f ( x ) ) : x ∈ K } m ∗ ( F ) = 0 m^*(F) = 0 m ∗ ( F ) = 0
思路 :由于 K K K f f f K K K f f f K K K ∣ x 1 − x 2 ∣ ⩽ δ |x_1-x_2|\leqslant \delta ∣ x 1 − x 2 ∣ ⩽ δ ∣ f ( x 1 ) − f ( x 2 ) ∣ ⩽ ε |f(x_1)-f(x_2)|\leqslant \varepsilon ∣ f ( x 1 ) − f ( x 2 ) ∣ ⩽ ε K K K π \pi π ∀ q ∈ π \forall q\in\pi ∀ q ∈ π diam q ⩽ δ \text{diam }q\leqslant \delta diam q ⩽ δ w q ⩽ ε w_q\leqslant \varepsilon w q ⩽ ε f ( q ) ⊂ I q f(q)\subset I_q f ( q ) ⊂ I q K × I q K\times I_q K × I q F F F m ∗ ( I q ) ⩽ ε m^*(I_q)\leqslant \varepsilon m ∗ ( I q ) ⩽ ε m ∗ ( F ) m^*(F) m ∗ ( F ) ε \varepsilon ε
推论 :Q ⊂ R n Q\subset \mathbb{R}^n Q ⊂ R n m ∗ ( ∂ Q ) = 0 m^*(\partial Q) = 0 m ∗ ( ∂ Q ) = 0
⟺ \iff ⟺ 设 Q ⊂ R n Q\subset \mathbb{R}^n Q ⊂ R n f : Q → R f:Q\rightarrow \mathbb{R} f : Q → R D ( f ) = { x ∈ Q : f 在 x 处不连续 } D(f) = \{x\in Q:f\text{在} x \text{处不连续}\} D ( f ) = { x ∈ Q : f 在 x 处不连续 } f R i e m a n n f\ Riemann f R i e m a n n ⟺ \iff ⟺ m ∗ ( D ( f ) ) = 0 m^*(D(f)) = 0 m ∗ ( D ( f ) ) = 0
证明方法和一维的推导方法类似。
推论 :若 f ∈ C ( Q ) f\in C(Q) f ∈ C ( Q ) f R i e m a n n f\ Riemann f R i e m a n n