PPO (Proximal Policy Optimization) 算法

参考文献：(1). Proximal Policy Optimization Algorithms - OpenAI, (2). Trust Region Policy Optimization - Berkeley，(3). Generalized Advantage Estimation - Berkeley

理论推导

基础定义

与概率论中记法一致，用大写字母表示随机变量，小写字母表示对应随机变量的观测值。

首先给出一些记号的定义：参考文献$^2$中的记法，将一阶Markov过程记为 $(S, A, P, R, \rho_0, \gamma)$，其中每一项分别表示：

• $\mathcal{S}$：策略空间。
• $\mathcal{A}$：动作空间。
• $P$：一阶Markov转移概率，$P:S\times A\to S$，通常记为 $P(s'|s,a)$ 表示从状态 $s$ 通过动作 $a$ 转移到状态 $s'$ 的概率大小。
• $R$：奖励函数，$R:\mathcal{S}\to \mathbb{R}$，表示达到状态 $S$ 所获得的奖励大小。
• $\rho(0)$：表示初始的状态分布空间，也就是一段轨迹中第一个状态所来自的分布 $S_0\sim \rho_0$。
• $\gamma$：表示折扣系数，$\gamma\sim (0,1)$。

记 $\pi(a|s)$ 为策略函数，$Q_{\pi}(s,a), V_{\pi}(s), D_{\pi}(s,a)$ 分别为动作价值函数、状态价值函数、优势价值函数，其定义如下：

$$\begin{aligned} Q_{\pi}(S_t,A_t) =&\ \mathbb{E}_{S_{t+1},A_{t+1},\cdots}\left[\sum_{i=0}^{\infty}\gamma^iR(S_{t+i+1})\right]\\ V_{\pi}(S_t) =&\ \mathbb{E}_{A_{t},S_{t+1},A_{t+1},\cdots}\left[\sum_{t=0}^{\infty}\gamma^tR(S_{t+1})\right] = \mathbb{E}_{A_{t}\sim\pi(\cdot|S_{t})}\left[Q_{\pi}(S_t,A_t)\right]\\ D_{\pi}(S_t,A_t) =&\ Q_{\pi}(S_t,A_t) - V_{\pi}(S_t) \end{aligned}$$

其中 $S_{t+1},A_{t+1},\cdots$ 满足 $\forall i\geqslant t$ 有 $S_{i+1}\sim P(\cdot|S_{i},A_{i}), A_{i+1}\sim\pi(\cdot|S_{i+1})$。

用 $\tau = (S_0,A_0,S_1,A_1,\cdots)\sim\pi$ 表示由策略 $\pi$ 与环境交互得到的一个轨迹，记 $R_t = R(S_{t+1})$，表示状态 $S_t$ 通过执行动作 $A_t$ 得到的奖励。

由Bellman方程可知 $Q_{\pi},V_{\pi}$ 之间的关系为

$$\begin{aligned} Q_{\pi}(S_t,A_t) =&\ \mathbb{E}_{S_{t+1}}\left[R(S_{t+1})+\gamma V_{\pi}(S_{t+1})\right]\\ =&\ \mathbb{E}_{S_{t+1},A_{t+1}}\left[R(S_{t+1}) + \gamma Q_{\pi}(S_{t+1},A_{t+1})\right] \end{aligned}$$

记 $\eta(\pi) = \mathbb{E}_{S\sim\rho_0}[V_{\pi}(S)]$ 为策略 $\pi$ 的期望折后回报，故可用 $\eta(\pi)$ 来衡量策略 $\pi$ 的好坏。

策略迭代

定理1 策略回报递推关系

设策略 $\tilde{\pi},\pi$，则

$$\eta(\tilde{\pi}) = \eta(\pi) + \mathbb{E}_{\tau\sim\tilde{\pi}}\left[\sum_{t=0}^{\infty}\gamma^tD_{\pi}(S_t,A_t)\right]$$

其中 $\tau = (S_0,A_0,S_1,A_1,\cdots)$ 表示由策略 $\tilde{\pi}$ 与环境交互得到的轨迹。

观察：该定理说明可以通过一个策略的折后回报估计另一个策略的折后回报，如果我们要得到比 $\pi$ 更优的策略 $\tilde{\pi}$ 则右式的第二项应该为正，所以我们期望最大化该项。

证明：（直接对优势函数进行分解即可）

$$\begin{aligned} &\ \mathbb{E}_{\tau\sim\tilde{\pi}}\left[\sum_{t=0}^{\infty}\gamma^tD_\pi(S_t,A_t)\right] = \mathbb{E}_{\tau\sim\tilde{\pi}}\left[\sum_{t=0}^{\infty}\gamma^t(Q_{\pi}(S_t,A_t) - V_{\pi}(S_t))\right] \\ \xlongequal{\text{Bellman方程}}&\ \mathbb{E}_{\tau\sim\tilde{\pi}}\left[\sum_{t=0}^{\infty}\gamma^t(R_t+\gamma V_{\pi}(S_{t+1})-V_{\pi}(S_t))\right]\\ =&\ \mathbb{E}_{\tau\sim\tilde{\pi}}\left[-V_{\pi}(S_0) + \sum_{t=0}^{\infty}\gamma^tR_t\right] = -\mathbb{E}_{S_0\sim \rho_0}\left[V_{\pi}(S_0)\right]+\mathbb{E}_{\tau\sim\tilde{\pi}}\left[\sum_{t=0}^{\infty}\gamma^tR_t\right]\\ =&\ -\eta(\pi) + \eta(\tilde{\pi}) \end{aligned}$$

---

推论1 策略回报参数形式

下式中的参数与定理1中相同：

$$\eta(\tilde{\pi}) = \eta(\pi) + \sum_{t=0}^{\infty}\sum_{S\in\mathcal{S}}\rho_{\tilde{\pi}}(S)\sum_{A\in\mathcal{A}}\tilde{\pi}(A|S)D_{\pi}(S,A)$$

其中 $\rho_{\tilde{\pi}}(S) = \sum_{t=0}^{\infty}\gamma^tP(S_t=S|\pi)$

对$\rho_{\pi}(S)$的理解：如果将 $\rho_{\pi}(S)$ 视为概率分布，则 $\rho_{\pi}(S)$ 表示由策略 $\pi$ 走出的轨迹中，状态 $S$ 出现的折后概率大小，如果 $\rho_{\pi}(S)$ 越大，说明 $S$ 在轨迹中前面几个时刻出现的概率越大。

证明：（只需注意随机变量的随机性来源）由定理1可知

$$\begin{aligned} \eta(\tilde{\pi}) =&\ \eta(\pi) + \mathbb{E}_{\tau\sim\tilde{\pi}}\left[\sum_{t=0}^{\infty}\gamma^tD_{\pi}(S_t,A_t)\right]\\ =&\ \eta(\pi) + \sum_{t=0}^{\infty}\sum_{S\in\mathcal{S}}P(S_t=S|\tilde{\pi})\sum_{A\in\mathcal{A}}\tilde{\pi}(A|S)\gamma^tD_{\pi}(S,A)\\ =&\ \eta(\pi)+\sum_{S\in\mathcal{S}}\sum_{t=0}^{\infty}\gamma^tP(S_t=S|\tilde{\pi})\sum_{A\in\mathcal{A}}\tilde{\pi}(A|S)D_{\pi}(S,A)\\ =&\ \eta(\pi) + \sum_{S\in\mathcal{S}}\rho_{\tilde{\pi}}(S)\sum_{A\in\mathcal{A}}\tilde{\pi}(A|S)D_{\pi}(S,A) \end{aligned}$$

---

当 $\pi\approx\tilde{\pi}$ 时，即 $\rho_{\pi}\approx\rho_{\tilde{\pi}}$，上式可表为

$$\tag{1.1} \eta(\tilde{\pi}) = \eta(\pi) + \sum_{t=0}^{\infty}\sum_{S\in\mathcal{S}}\rho_{\pi}(S)\sum_{A\in\mathcal{A}}\tilde{\pi}(A|S)D_{\pi}(S,A)$$

写成上式的形式可以用Monte-Carlo方法（MC方法）对其进行估计，注意到：

$$\begin{aligned} \tag{1.2} \sum_{S\in\mathcal{S}}\rho_{\pi(S)}[\cdots] =&\ \frac{1}{1-\gamma}\mathbb{E}_{S\sim\rho_{\pi}}[\cdots]\\ \sum_{A\in\mathcal{A}}\tilde{\pi}(A|S)[\cdots] =&\ \sum_{A\in\mathcal{A}}\pi(A|S)\frac{\tilde{\pi}(A|S)}{\pi(A|S)}[\cdots] = \mathbb{E}_{A\sim\pi}\left[\frac{\tilde{\pi}(A|S)}{\pi(A|S)}[\cdots]\right] \end{aligned}$$

上式中第一个式子是先将 $\rho_{\pi}(\cdot)$ 视为 $\mathcal{S}$ 上的概率密度函数，由于

$$\sum_{S\in\mathcal{S}}\rho_{\pi}(S) = \sum_{S\in\mathcal{S}}\sum_{t=0}^{\infty}\gamma^tP(S_t=S|\pi) = \sum_{t=0}^{\infty}\gamma^t\sum_{S\in\mathcal{S}}P(S_t=S|\pi) = \sum_{t=0}^{\infty}\gamma^t = \frac{1}{1-\gamma}$$

所以先要乘上归一化系数 $\rho_{\pi}(S)\gets (1-\gamma)\rho_{\pi}(S)$，故 $(1.2)$ 式要乘 $\frac{1}{1-\gamma}$ 使等式成立。

策略迭代 最优化目标

用神经网络表示 $\tilde{\pi},\pi$：记 $\begin{cases}\tilde{\pi}(a|s) =: \pi(a|s;\theta) =: \pi,\\ \pi(a|s)=:\pi(a|s;\theta^-)=:\pi^-\end{cases}$，这里 $\theta,\theta^-$ 分别表示策略 $\pi,\pi^-$ 对应的神经网络的参数（这里 $\pi,\pi^-$ 的网络结构一致）。这里我们假设 $\pi^-$ 已知（一般是 $\pi$ 的上一个迭代的参数，所以文献$^{1,2}$中也记为 $\pi_{\text{old}}$），期望能够最大化 $\eta(\pi)$。

策略迭代的带约束最优化目标 (Conservative Policy Iteration, CPI, 文献$^1$中记法)：

$$\begin{aligned} \tag{1.3} \max_{\theta}&\quad \mathcal{L}^{CPI}(\theta):= \eta(\pi(\theta))\propto\mathbb{E}_{S\sim\rho_{\pi^-}}\mathbb{E}_{A\sim\pi^-}\left[\frac{\tilde{\pi}(A|S;\theta)}{\pi(A|S;\theta^-)}D_{\pi^-}(S,A)\right]\\ s.t.&\quad \mathbb{E}_{S\sim\rho_{\pi^-}}\left[D_{KL}(\pi(\cdot|S;\theta^-)||\pi(\cdot|S;\theta))\right]\leqslant \varepsilon \end{aligned}$$

这里限制条件为 $\pi,\pi^-$ 的KL散度不超过给定的容许限制 $\varepsilon$。

于是可以用MC方法的对目标函数进行估计

$$\mathcal{L}^{CPI}(\theta) \approx \frac{1}{T}\sum_{(s_t,a_t)\sim\tau}\frac{\pi(a_t|s_t;\theta)}{\pi(a_t|s_t;\theta^-)}D_{\pi^-}(s,a)$$

其中 $\tau=(s_0,a_0,\cdots,s_T,a_T)\sim\pi^-$ 是策略 $\pi^-$ 走出的长度为 $T$ 的轨迹，但是这样估计是有偏的，因为 $S\sim\rho_{\pi^-}$ 并不是在整个轨迹上的均匀采样，而是加权后的分布，越靠近初始时刻权重越大，而这里的误差应该可以由GAE缓解（文献$^3$）。

---

有了目标函数的估计，下面就是如何求解带约束方程 $(1.3)$：

1. TRPO（置信域策略优化）直接通过共轭梯度法+线性搜索对其直接求解，复杂，低效。
2. PPO（近似策略优化）通过加入clip函数或惩罚项，将带约束问题转化为无约束问题，简单，高效。

PPO算法

这里只介绍基于clip函数的PPO算法，也就是文献$^1$中的第一个版本，第二个版本将 $\pi,\pi^-$ 的KL散度作为惩罚项，效果不如第一个版本，就不介绍了。

二者本质都是对$(1.3)$式的约束项（策略的近似度）的“惩罚”。

策略损失函数(Actor)

首先重写$(1.3)$式目标方程：

$$\begin{aligned} \mathcal{L}^{CPI}(\theta) =&\ \mathbb{E}_{S\sim\rho_{\pi^-}}\mathbb{E}_{A\sim\pi^-}\left[\frac{\tilde{\pi}(A|S;\theta)}{\pi(A|S;\theta^-)}D_{\pi^-}(S,A)\right] = \mathbb{E}_t\left[\frac{\pi(A_t|S_t;\theta)}{\pi(A_t|S_t;\theta^-)}D_t\right]\\ =&\ \mathbb{E}_t[\xi_t(\theta)D_t] \end{aligned}$$

其中 $\xi_t(\theta) := \dfrac{\pi(A_t|S_t;\theta)}{\pi(A_t|S_t;\theta^-)}$，这一项可以被用来衡量策略 $\pi,\pi^-$ 的近似程度，如果 $\mathbb{E}_t[\xi_t(\theta)]\to 1$，则说明 $\pi\approx\pi^-$，而PPO的clip函数损失函数就是这么做的。

当 $\xi_t(\theta)$ 超过范围 $(1-\varepsilon,1+\varepsilon)$ 时，说明 $\pi,\pi^-$ 的差距过大，则不对 $\theta$ 进行更新，据此构造新的无约束优化目标：

$$\max_{\theta}\quad\mathcal{L}^{CLIP}(\theta) := \mathbb{E}_{t}\left[\min\bigg\{\xi_t(\theta)D_t,\text{clip}\big(\xi_t(\theta),1-\varepsilon,1+\varepsilon\big)D_t\bigg\}\right]$$

其中 $\text{clip}(x,a,b) = \begin{cases} a,&\quad x\in[b,\infty),\\ x,&\quad x\in [a,b),\\ b,&\quad x\in(-\infty,a), \end{cases}$，我将 $L^{CLIP}$ 与 $\xi$ 的关系，分 $D>0$ 和 $D<0$ 两种情况讨论，如下图所示：

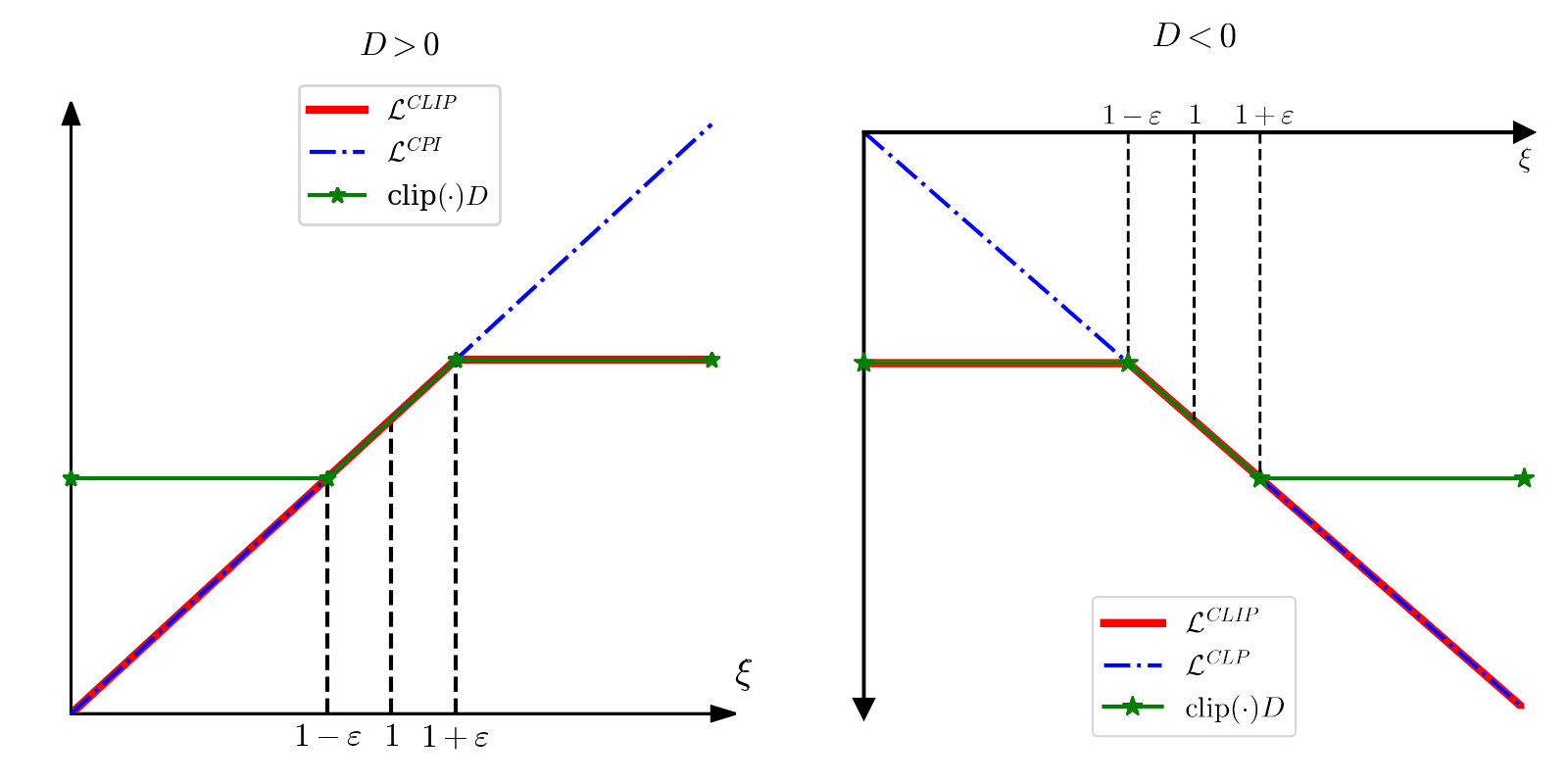
绘制右图代码

import numpy as np
import matplotlib.pyplot as plt
config = {
    "font.family": 'serif', # 衬线字体
    "figure.figsize": (5, 5),  # 图像大小
    "font.size": 14, # 字号大小
    "font.serif": ['SimSun'], # 宋体
    "mathtext.fontset": 'cm', # 渲染数学公式字体
    'axes.unicode_minus': False # 显示负号
}
plt.rcParams.update(config)

fig, ax = plt.subplots()
# 关闭默认坐标轴右侧和上侧的边框
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
# 将左侧和底侧的边框固定在零上, 设置线宽度为2
ax.spines['left'].set_position('zero')
ax.spines['left'].set_linewidth(2)
ax.spines['bottom'].set_position('zero')
ax.spines['bottom'].set_linewidth(2)
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
# 关闭刻度
ax.set_xticks([])
ax.set_yticks([])
# 设置显示(x_min, x_max, y_min, y_max)范围
ax.axis([0, 2, -2, 0])
# 设置箭头符号
ax.plot(2, 0, ls="", marker=">", ms=10, color="k", clip_on=False)
ax.plot(0, -2, ls="", marker="v", ms=10, color="k", clip_on=False)

eps = 0.2
ax.plot([0, 1-eps], [-1+eps, -1+eps], 'r', label=r"$\mathcal{L}^{CLIP}$", lw=4)
ax.plot([1-eps, 2], [-1+eps, -2], 'r', lw=4)
ax.plot([0, 2], [0, -2], 'b-.', label=r"$\mathcal{L}^{CLP}$", lw=2)
ax.plot([0, 1-eps], [-1+eps, -1+eps], 'g*-', label=r"$\text{clip}(\cdot)D$", clip_on=False, zorder=3, lw=2, ms=10)
ax.plot([1-eps, 1+eps], [-1+eps, -1-eps], 'g*-', lw=2, ms=10)
ax.plot([1+eps, 2], [-1-eps, -1-eps], 'g*-', clip_on=False, lw=2, ms=10)
ax.plot([1-eps, 1-eps], [0, -1+eps], 'k--', lw=1.5)
ax.plot([1, 1], [0, -1], 'k--', lw=1.5)
ax.plot([1+eps, 1+eps], [0, -1-eps], 'k--', lw=1.5)

ax.text(1-eps-0.08, 0.03, r"$1-\varepsilon$")
ax.text(1-0.02, 0.03, r"$1$")
ax.text(1+eps-0.08, 0.03, r"$1+\varepsilon$")
ax.text(2-0.02, -0.12, r"$\xi$")
fig.suptitle("$D<0$")
fig.legend(loc="lower center")
fig.tight_layout()
plt.savefig("ppo_D_neg.png", dpi=300)
plt.show()

价值损失函数(Critic)

第二个问题：$D_t$ 如何估计？和A2C的方法相同，用神经网络 $v(s;w)$ 近似 $V_\pi(s)$，其中 $w$ 为神经网络的参数，则

$$\tag{2.1} \begin{aligned} D_t =&\ \mathbb{E}_{S_t,A_t}\big[Q_{\pi^-}(S_t,A_t) - V_{\pi^-}(S_t)\big] \\ =&\ \mathbb{E}_{S_t,A_t,S_{t+1}}\big[R_t + \gamma V_{\pi^-}(S_{t+1})-V_{\pi^-}(S_t)\big]\\ \text{(TD)}\approx&\ r_t + \gamma v(s_{t+1};w^-) - v(s_t;w^-) = \delta_t\\ \text{(MC)}\approx&\ -v(s_{t};w^-) + r_t + \gamma r_{t+1} + \cdots + \gamma^{T-t+1}r_{T-1} + \gamma^{T-t}v(s_T;w^-)\\ \text{(MC)}=&\ \delta_t + \gamma\delta_{t+1} + \cdots + \gamma^{T-t+1}\delta_{T-1} \end{aligned}$$

其中第三行为TD估计，第四五行为MC估计，$\delta_t = r_t + \gamma v(s_{t+1};w^-) - v(s_t;w^{-})$，这个 $\delta_t$ 和Q-Learning中的TD误差有点类似，TD误差定义是

$$\delta^{TD}_t = v(s_t;w) - (r_t + \gamma v(s_{t+1};w^-))$$

注意$(2.1)$式中$S_t\sim \rho_{\pi^-}$，所以 $S_t$ 还是带有对轨迹进行加权平均后的概率分布，越靠近初始时刻系数越大。这就要引入GAE（Generalized Advantage Estimation，文献$^3$）对其进行估计（这其实也是对TD和MC估计的一个综合，$\lambda=0$ 时为TD估计，$\lambda=1$ 时为MC估计）：

$$\tag{2.2} \hat{D}_t = \delta_t + (\gamma\lambda)\delta_{t+1}+\cdots+(\gamma\lambda)^{T-t+1}\delta_{T-1}$$

其中 $\lambda$ 称为GAE系数，GAE本质上是TD-$\lambda$的应用。

---

对参数 $w$ 的更新可由Bellman方程推出，关于状态价值函数的Bellman方程如下：

$$\mathbb{E}_{S_t}\big[V_{\pi}(S_t)\big] = \mathbb{E}_{S_t,A_t,S_{t+1}}\big[R_t+\gamma V_{\pi}(S_{t+1})\big]$$

则TD估计为 $V_{\pi}(s_t)\approx r_t + \gamma V_{\pi}(s_{t+1})$，但这里可以利用更好的估计 $D_t + V_{\pi}(s_t)$，因为它是综合了TD和MC方法的估计，所以应具有更小的方差，更稳定，为了避免偏差的传递，可以利用DDQN中目标网络的方法，构造出以下价值函数的最优化目标(Value Function, VF, 文献$^1$中记法)：

$$\min_{w}\quad \mathcal{L}^{VF}:= \mathbb{E}_t\bigg[\big|D_t + v(S_t;w^-) - v(S_t;w)\big|^2\bigg]$$

鼓励探索性(Regular)

最后一个问题：如何鼓励智能体去探索新的策略？

也就是说不要使决策过于绝对，用信息熵表示就是 $\text{Entropy}\big[\pi(\cdot|S)\big], \forall S\in\mathcal{S}$ 不能过小，所以可以构造信息熵正则项：

$$\max_{\theta}\quad \mathcal{L}^{ENT}(\theta):= \mathbb{E}_t\bigg[\text{Entropy}\big[\pi(\cdot|S)\big]\bigg] = \mathbb{E}_t\left[-\sum_{a\in\mathcal{A}}\pi(a|S_t;\theta)\ln\pi(a|S_t;\theta)\right]$$

总损失函数

综上，我们得到了PPO算法的损失函数如下：

$$\min_{\theta,w}\quad \mathcal{L}^{PPO}(\theta,w) = -\mathcal{L}^{CLIP}(\theta) + c_1\mathcal{L}^{VF}(w) - c_2\mathcal{L}^{ENT}(\theta)$$

其中 $c_1,c_2$ 分别为的对应损失函数的系数。

代码实现

在自己设计的RL框架下，使用TF2实现，参考了cleanrl强化学习框架的PPO代码：ppo.py - cleanrl GitHub，还有其对应的讲解视频：PPO Implementation - YouTube（但他是用PyTorch实现的）

实现的是多线程的PPO，对于CartPole环境训练30s就能得到最优策略，原代码：PPO.py

实现细节

主要难点在于Actor的写法，我采用 np.ndarray 记录Actor在每个时刻 $t$ 下的信息，该部分需要记录：

• 四元组 $(S,A,R,S')$：状态 $S_t$，执行动作 $A_t$，得到奖励 $R_t$，以及下一个状态 $S_{t+1}$。
• 终止标记 $T$：$T_t$ 表示 $S_{t+1}$ 是否为终止状态。
• 优势函数(GAE) $AD$：$AD_t = \sum_{i=0}^{T-t-1}(\gamma\lambda)^{i}\delta_{t+i} \cdot T_{t+i}$，与$(2.2)$式一致。
• 目标价值 $V$：$V_t = AD_t + v(s_t;w^-)$.
• 对数策略分布 $LP$：$LP_t = \ln\big(\pi(a_t|s_t;\theta^-)\big)$

需要注意的细节是计算 $AD$ 时，终止状态无需加后继的 $\delta$，否则会加到初始状态上，导致结果错乱，并且还需计算最后一个状态 $s_T$ 对应的价值函数 $v(s_T;w^-)$。

这部分的正确写法就是使用 numpy，使用 jax 中的数据结构保存到显存中，只会因为IO频率过高导致降速，除非能够直接将环境编译到XLA中，也就是 envpool 的实现效果。（这部分在numpy上已测试过）

numpy的memory_buffer实现

S, A, R, S_, T, AD, V, LP = \  # initialize array
    np.zeros(shape=(self.T, self.N) + state_shape, dtype='float32'), \
    np.zeros(shape=(self.T, self.N) + action_shape, dtype='int32'), \
    np.zeros(shape=(self.T, self.N), dtype='float32'), \
    np.zeros(shape=(self.T, self.N) + state_shape, dtype='float32'), \
    np.zeros(shape=(self.T, self.N), dtype='bool'), \
    np.zeros(shape=(self.T, self.N), dtype='float32'), \
    np.zeros(shape=(self.T, self.N), dtype='float32'), \
    np.zeros(shape=(self.T, self.N), dtype='float32')

for step in range(self.T):
    v, proba = self.pred(self.state)
    V[step] = v.numpy().squeeze()  # save state value
    action = sample_from_proba(proba.numpy())
    action_one_hot = make_onehot(action, depth=self.env.action_size).astype('bool')
    LP[step] = np.log(proba[action_one_hot])  # ln policy probability
    state_, reward, terminal = self.env.step(action)
    action = action.reshape(-1, 1)
    S[step], A[step], R[step], S_[step], T[step] = \  # 5-tuple
        self.state, action, reward, state_, terminal
    self.state = state_
v_last, _ = self.pred(self.state)
v_last = v_last.numpy().reshape(1, self.N)
# Calc Delta Value
AD = R + self.gamma * np.r_[V[1:,:], v_last] * (~T) - V
# Calc Advantage Value
for i in reversed(range(self.T-1)):
    AD[i] += self.gamma * self.lambda_ * AD[i+1] * (~T[i])
# Target state value
V += AD

第二个在于训练函数 train_step 的写法：

jax的train_step写法

@partial(jax.jit, static_argnums=0)
def train_step(self, state:TrainState, dataset, idxs):
    def loss_fn(params, dataset, idxs):
        s, a, ad, v, logpi = jax.tree_map(lambda x: x[idxs], dataset)
        v_now, logits = self.model.state.apply_fn(params, s)
        loss_v = ((v_now - v - ad) ** 2).mean() / 2

        if self.args.flag_ad_normal:
            ad = (ad - ad.mean()) / (ad.std() + self.args.EPS)

        logpi_now = jax.nn.log_softmax(logits)[jnp.arange(a.shape[0]), a.flatten()].reshape(-1, 1)
        rate = jnp.exp(logpi_now - logpi)
        loss_p = jnp.minimum(
            ad * rate,
            ad * jnp.clip(
                rate,
                1 - self.args.epsilon,
                1 + self.args.epsilon
            )
        ).mean()

        loss_entropy = - (jax.nn.log_softmax(logits) * jax.nn.softmax(logits)).sum(-1).mean()

        loss = - loss_p \
               + self.args.coef_value * loss_v \
               - self.args.coef_entropy * loss_entropy
        return loss, (v, ad, loss_p, loss_v, loss_entropy)

    (loss, metrics), grads = jax.value_and_grad(loss_fn, has_aux=True)(state.params, dataset, idxs)
    state = state.apply_gradients(grads=grads)
    return state, metrics

tensorflow的train_step写法

第二个重点在于 @tf.function 的写法

@tf.function
def train_step(self, s, a, ad, v, logpi):
    with tf.GradientTape() as tape:
        v_now, p_now = self.model(s)
        loss_v = tf.square(v_now-v-ad)
        if self.flag_clip_value:  # 是否对value进行裁剪，默认不需要，因为效果并不明显
            loss_v_clip = tf.square(
                tf.clip_by_value(
                    v_now - v,
                    clip_value_min=-self.v_epsilon,
                    clip_value_max=self.v_epsilon
                )-ad
            )
            loss_v = tf.maximum(loss_v, loss_v_clip)
        loss_v = tf.reduce_mean(loss_v / 2)  # value loss function

        if self.flag_ad_normal:  # 优势函数正则化
            mean, var = tf.nn.moments(ad, axes=[0])
            ad = (ad - mean) / (var + EPS)

        logpi_now = tf.math.log(tf.reshape(p_now[a], (-1, 1)))
        lograte = logpi_now - logpi
        rate = tf.math.exp(lograte)  # 计算策略比例大小
        loss_p_clip = tf.reduce_mean(  # 计算裁剪policy loss
            tf.minimum(
                rate*ad,
                tf.clip_by_value(
                    rate,
                    clip_value_min=1-self.epsilon,
                    clip_value_max=1+self.epsilon
                )*ad
            )
        )
        loss_entropy = -tf.reduce_mean(  # 交叉熵正则化
            tf.reduce_sum(p_now*tf.math.log(p_now), axis=1)
        )
        loss = - loss_p_clip \  # 总损失函数
               + self.coef_value * loss_v \
               - self.coef_entropy * loss_entropy
    grads = tape.gradient(loss, self.model.get_trainable_weights())
    self.model.apply_gradients(grads)
    return tf.reduce_mean(v_now), loss_p_clip, loss_v, loss_entropy

1. 一定要实现线性学习率下降，否则网络参数会发散。

测试结果

KataRL中用JAX实现PPO的代码ppo_jax.py，线性模型超参数文件，atari环境超参数文件，PPO在所有环境上均碾压其他算法：不同环境下算法比较。使用方法：

python katarl/run/ppo/ppo.py --train --wandb-track --capture-video
python katarl/run/ppo/ppo.py --train --wandb-track --capture-video --env-name Acrobot-v1 
python katarl/run/ppo/atari_ppo.py --train --wandb-track --capture-video

总共16个超参数（CartPole超参数为例）：

gamma = 0.99  # discount rate
lambda_ = 0.95  # GAE parameter
epsilon = 0.2  # clip epsilon
v_epsilon = 1  # value clip epsilon
actor_N = 8  # Actor number > 1
frames_M = int(2e5)  # Total frames
step_T = 512  # move steps
epochs = 5  # train epochs
batch_size = 32
coef_value = 1  # coef of value loss
coef_entropy = 0.01  # coef of entropy regular
flag_ad_normal = True  # Whether normalize advantage value
flag_clip_value = False  # Whether clip the ad value
init_lr = 3e-4  # init learning rate
flag_anneal_lr = True  # anneal learning rate
EPS = 1e-8

CartPole

30s能够达到最大的步数（500step），以上超参数训练结果，总共重启30次，每次训练用时5分钟。

Breakout

用时6h能够完成一次训练，效率还是很低，远不如jax+envpool，有待更新算法，训练轨迹如下：