CF1793 - Codeforces Round
最新更新于: 2024年5月24日上午11点17分
Codeforces Round #852 (Div. 2)
F. Rebrending
题意
区间长度为的数组,且满足,有个查询区间,对于每个查询区间,求出
中相差最小的值,即
思路
该题不好直接构造线段树维护差值最小值,考虑离线做法.
令当前考虑右端点在 处的查询 ,设 为 与 的最小差值,即 .
从左到右依次扫描 ,考虑如何使用 更新 的dp值.
设 为距离 最近且比 大的值,若 且 ,则 离 的距离不低于 ,所以无需更新. 所以要找
依此类推:
直到 或者 ,于是我们只需更新 的dp值为 .
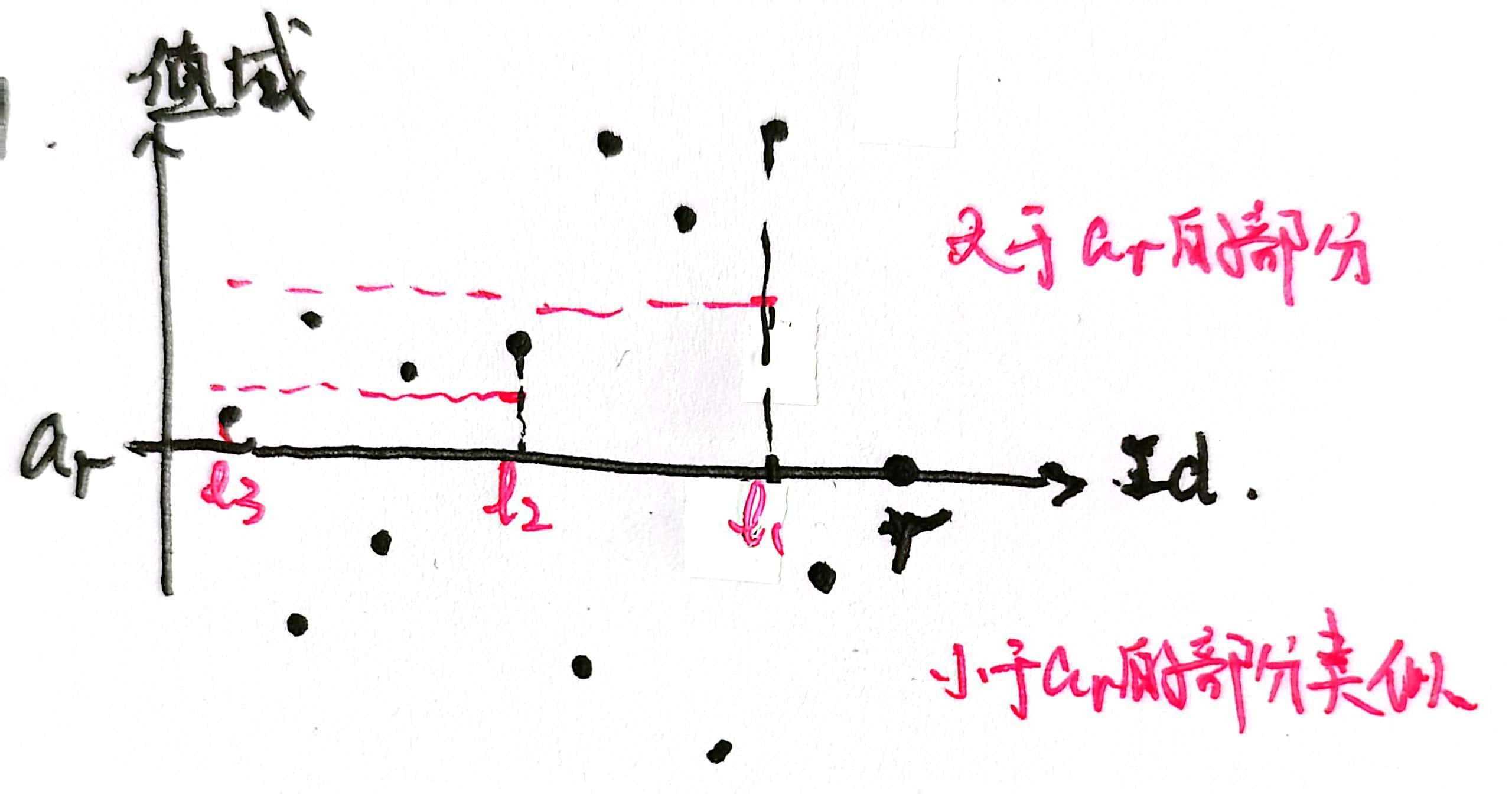
对于 与 处理类似,只需找
由于值域为 则更新节点数为 ,用线段树查找 用时 ,总计用时 .
对于每个询问 ,当右端点 时,答案为 ,用另一颗线段树记录dp值即可,用时 .
具体算法步骤:
- 离线全部询问,以右端点进行排序.
- 构造两颗线段树:
- key: Id, value: dp值,找区间最小值
- key: ,value: Id,找区间最大值.
点击显/隐代码
/*
* File : F.cpp
* Time : 2023/02/17 15:56:24
* Author : wty-yy
* Version : 1.0
* Blog : https://wty-yy.space/
* Desc : https://codeforces.com/contest/1793/problem/F
*/
#include <iostream>
#include <algorithm>
#include <cstring>
#include <math.h>
#include <vector>
#include <map>
#define ll long long
#define ls (p << 1)
#define rs (p << 1 | 1)
using namespace std;
const int N = 3e5 + 10;
const int Q = 1e6 + 10;
const int MAX = 0x7FFFFFFF;
const int MIN = -MAX;
int n, q, dp[N], a[N], ans[Q];
struct SegmentTree {
int mn[N<<2], mx[N<<2];
void init(int n) {
for (int i = 1; i <= 4*n; i++) {
mx[i] = MIN;
mn[i] = MAX;
}
}
void pushup(int p) {
mn[p] = min(mn[ls], mn[rs]);
mx[p] = max(mx[ls], mx[rs]);
}
void change(int p, int l, int r, int x, int val) {
if (l == x && r == x) {
mn[p] = min(mn[p], val);
mx[p] = max(mx[p], val);
return;
}
int mid = (l + r) >> 1;
if (x <= mid) change(ls, l, mid, x, val);
else change(rs, mid + 1, r, x, val);
pushup(p);
}
int get(int p, int l, int r, int L, int R, bool is_max) {
if (r < L || l > R) return is_max ? MIN : MAX;
if (l >= L && r <= R) return is_max ? mx[p] : mn[p];
int mid = (l + r) >> 1;
if (R <= mid) return get(ls, l, mid, L, R, is_max);
else if (L > mid) return get(rs, mid + 1, r, L, R, is_max);
else {
int vl = get(ls, l, mid, L, mid, is_max), vr = get(rs, mid + 1, r, mid + 1, R, is_max);
return is_max ? max(vl, vr) : min(vl, vr);
}
}
}seg_dp, seg_id;
struct Query {
int id, l, r;
bool operator < (Query b) { return r < b.r; }
}query[Q];
void update(int r, bool is_big) { // 用a[r]更新[1,...,r-1]的dp值,最多更新logn个
int L = is_big ? a[r] : MIN, R = is_big ? MAX : a[r], l;
while (1) {
l = seg_id.get(1, 1, n, L, R, 1);
if (l == MIN || l == MAX) break;
dp[l] = min(dp[l], abs(a[l] - a[r]));
seg_dp.change(1, 1, n, l, dp[l]);
if (a[l] == a[r]) break;
if (is_big) R = (a[l] + a[r]) >> 1;
else L = (a[l] + a[r] + 1) >> 1;
}
}
int main() {
memset(dp, 0x3f, sizeof(dp));
scanf("%d %d", &n, &q);
seg_dp.init(n), seg_id.init(n);
for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
for (int i = 0; i < q; i++) {
scanf("%d %d", &query[i].l, &query[i].r);
query[i].id = i;
}
sort(query, query + q);
int i = 0, r = 1;
while (i < q) {
update(r, 0); update(r, 1);
while (i < q && query[i].r == r) {
ans[query[i].id] = seg_dp.get(1, 1, n, query[i].l, query[i].r, 0);
i++;
}
seg_id.change(1, 1, n, a[r], r);
r++;
}
for (int i = 0; i < q; i++) printf("%d\n", ans[i]);
return 0;
}CF1793 - Codeforces Round
https://wty-yy.xyz/posts/39924/