SAC (Soft Actor-Critic) 算法

概述

SAC算法可以简单理解为一种将Q-Learning用于策略 $\pi_{\theta}(a|s)$ 估计的算法，由于使用了策略网络，所以可以用于解决连续问题，与梯度策略定理(A2C)或策略迭代定理(TRPO,PPO)不同，SAC策略网路的更新目标浅显易赅，就是要近似 $Q_{\pi^*}(s,\cdot)$ 对应的 softmax 分布，不过这里的价值状态函数还引入了熵正则项，直观理解就是将原有的奖励 $r_t$ 的基础上加入了下一个状态的信息熵，从而变为 $r_t^{\pi} := r_t + \gamma \alpha \mathcal{H}(\pi(\cdot|s_{t+1}))$（其中 $\alpha$ 为温度系数，$\mathcal{H}$ 为信息熵），我们可以用下图来对其进行直观理解，其中红色部分就是SAC折后回报所包含的项：

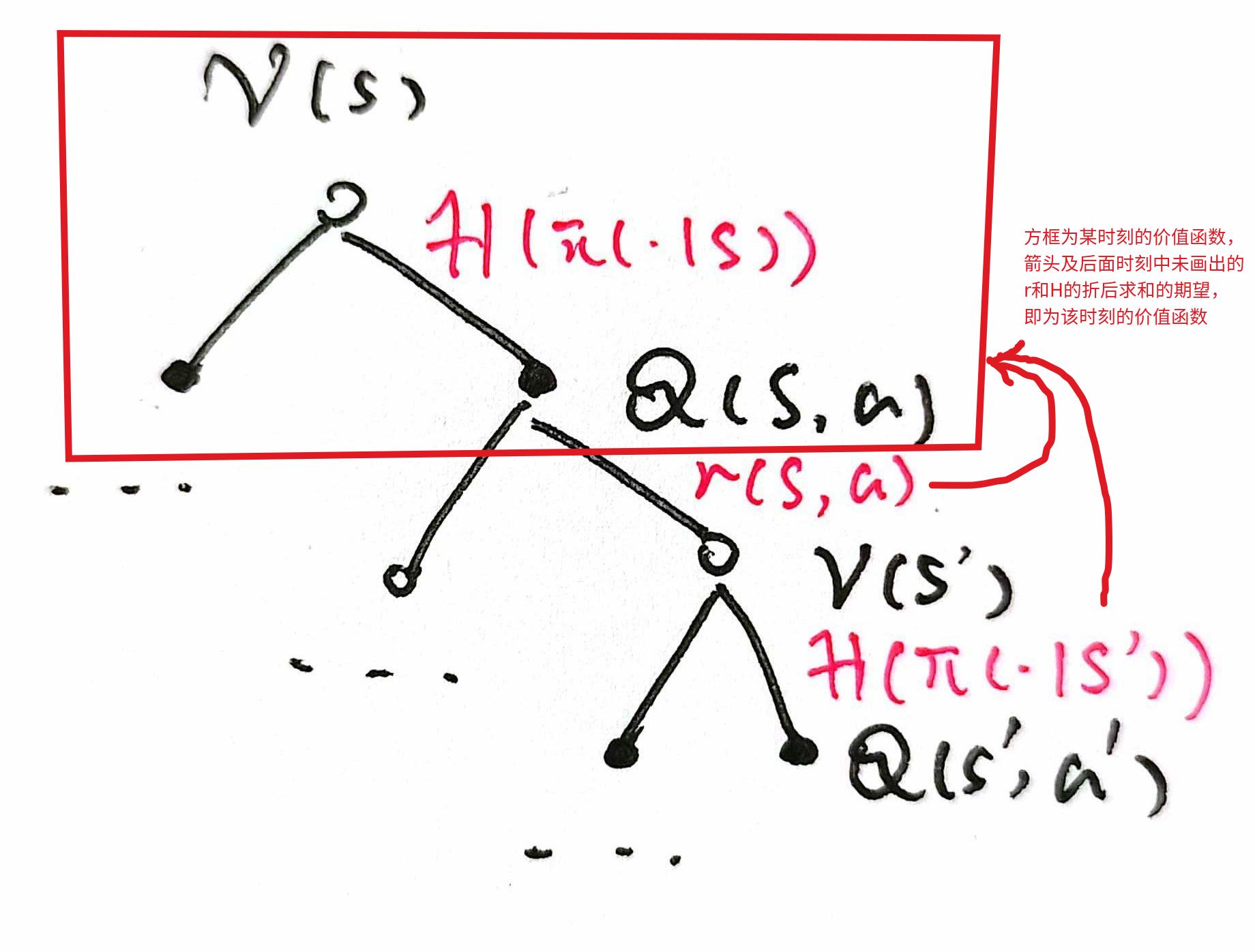
参考文献：1. Soft Actor-Critic Algorithms and Applications

理论推导

定义1（软价值函数 soft-value function）

定义策略 $\pi$ 的软动作价值函数和软状态价值函数如下：

$$\begin{aligned} Q_{\pi}(s_t,a_t) =& \mathbb{E}_{\rho_{t+1}\sim\pi}\left[\sum_{i=t}^{\infty}\gamma^{i-t}(R_i+\gamma\alpha\mathcal{H}(\pi(\cdot|S_{t+1})))|S_t=s_t,A_t=a_t\right]\\ =& \mathbb{E}_{\rho_{t+1}\sim\pi}\left[\sum_{i=t}^{\infty}\gamma^{i-t}(R_i-\gamma\alpha\log\pi(A_{i+1}|S_{i+1}))|S_t=s_t,A_t=a_t\right]\\ V_{\pi}(s_t) =& \mathbb{E}_{\rho_{t+1}\sim\pi}\left[\sum_{i=t}^{\infty}\gamma^{i-t}(R_i+\gamma\alpha\mathcal{H}(\pi(\cdot|S_{t+1})))|S_t=s_t\right]\\ \end{aligned}$$

且有 $V(s_t) = \mathbb{E}_{A_t\sim\pi(\cdot|s_t)}[Q(s_t, A_t)]$。

定义2（SAC最优化目标）

SAC算法的目标为最大化带有熵正则的折后回报：

$$\pi^* = \argmax_{\pi}\mathbb{E}_{\rho\sim\pi}\left[\sum_{t=0}^{\infty}\gamma^{i-t}(R_t + \gamma\alpha\mathcal{H}(\pi(\cdot|S_{t+1})))\right] = \argmax_{\pi}\mathbb{E}_S[V_{\pi}(S)]$$

其中 $\rho = (S_0,A_0,S_1,A_1,\cdots)$ 为一幕序列，$\rho\sim\pi$ 表示 $A_t\sim \pi(\cdot|S_t),\ \forall t \geqslant 0$，$\alpha$ 为温度系数，$\gamma\in(0,1)$ 为折扣率。

定理3（状态价值估计）

$$\begin{aligned} \text{原Bellman方程：} Q_{\pi}(s_t,a_t) =&\ \mathbb{E}_{S_{t+1},A_{t+1}}[R_t+\gamma Q_{\pi}(S_{t+1},A_{t+1})|s_t,a_t]\\ \text{软Bellman方程：} Q_{\pi}(s_t,a_t) =&\ \mathbb{E}_{S_{t+1},A_{t+1}}[R_t+\gamma\alpha\mathcal{H}(\pi(\cdot|S_{t+1}))+\gamma Q_{\pi}(S_{t+1},A_{t+1})|s_t,a_t]\\ =&\ R_t + \gamma\mathbb{E}_{S_{t+1},A_{t+1}}[Q_{\pi}(S_{t+1},A_{t+1}) - \alpha\log\pi(A_{t+1}|S_{t+1})] \end{aligned}$$

故可通过TD-1的方法对 $Q_{\pi}(s,a)$ 进行估计。

证明：只需将原Bellman方程中的 $R_t$ 换成 $R_t + \gamma\alpha\mathcal{H}(\pi(\cdot|S_{t+1}))$ 即可。

---

定理4（策略更新）

对于一列策略 $\{\pi_{k}\}$，若其满足一下递推关系：

$$\pi_{k+1}\gets \argmin_{\pi} D_{KL}\left(\pi(\cdot|s)\bigg|\bigg|\frac{\exp(\frac{1}{\alpha}Q_{\pi_k}(s,\cdot))}{Z_{\pi_k}(s)}\right), \quad(k\in\mathcal{N})$$

其中 $Z_{\pi_k}(s) = \sum_{a\in\mathcal{A}}\exp(\frac{1}{\alpha}Q_{\pi_k}(s,\cdot))$ 及归一化系数（partition function），若 $\pi_k$ 收敛，则 $\pi_k$ 收敛到定义2中最优化目标的一个局部最优解。

观察：该定理告诉我们 $\pi$ 的更新方向就是当前 $Q_{\pi}(\cdot|s)$ 对应的softmax分布。

证明：（对KL散度进行拆分化减，在利用Bellman方程进行迭代证明，该证明类似Q-Learning中对Q函数迭代更新的证明）

$$\begin{aligned} J_{\pi}(\pi_k):=&\ D_{KL}\left(\pi(\cdot|s)\bigg|\bigg|\frac{\exp(\frac{1}{\alpha}Q_{\pi_k}(s,\cdot)}{Z_{\pi_k}(s)}\right)\\ =&\ D_{KL}\big(\pi(\cdot|s)||\exp(\tfrac{1}{\alpha}Q_{\pi_k}(s,\cdot) - \log Z_{\pi_k}(s))\big)\\ =&\ \mathbb{E}_{a\sim\pi(\cdot|s)}\big[\log\pi(a|s) - \tfrac{1}{\alpha}Q_{\pi_k}(s,a)+\log Z_{\pi_k}(s)\big] \end{aligned}$$

又由于 $J_{\pi_{k+1}}(\pi_k)\leqslant J_{\pi_k}(\pi_k)$，则

$$\begin{aligned} \mathbb{E}_{a\sim\pi_{k+1}(\cdot|s)}\big[\log\pi_{k+1}(a|s) - \tfrac{1}{\alpha}Q_{\pi_k}(s,a) +&\ \log Z_{\pi_k}(s)\big] \\ \leqslant \mathbb{E}_{a\sim\pi_{k}(\cdot|s)} \big[\log\pi_{k}(a|s) -&\ \tfrac{1}{\alpha}Q_{\pi_k}(s,a) + \log Z_{\pi_k}(s)\big]\\ \Rightarrow \mathbb{E}_{a\sim\pi_{k+1}(\cdot|s)}\big[\log\pi_{k+1}(a|s) - \tfrac{1}{\alpha}Q_{\pi_k}(s,a)\big] \leqslant &\ \mathbb{E}_{a\sim\pi_{k}(\cdot|s)}\big[\log\pi_{k}(a|s) - \tfrac{1}{\alpha}Q_{\pi_k}(s,a)\big]\\ \leqslant &\ -\frac{1}{\alpha}\mathbb{E}_{a\sim\pi_k(\cdot|s)}(Q_{\pi_k}(s,a)) = -\frac{1}{\alpha}V_{\pi_k}(s)\\ \Rightarrow V_{\pi_k}(s)\leqslant \mathbb{E}_{a\sim\pi_{k+1}(\cdot|s)}[Q_{\pi_k}(s,a) - \alpha\log\pi_{k+1}&\ (a|s)] \end{aligned}$$

于是 $\forall (s_t,a_t)\in \mathcal{S}\times \mathcal{A}$ 有

$$\begin{aligned} Q_{\pi_k}(s_t,a_t) =&\ \mathbb{E}_{S_{t+1}\sim p(\cdot|s_t,a_t)}[R_t + \gamma V_{\pi_k}(S_{t+1})]\\ \leqslant&\ \mathbb{E}_{\substack{S_{t+1}\sim p(\cdot|s_t,a_t)\\A_{t+1}\sim \pi_{k+1}}}[R_t + \gamma Q_{\pi_k}(S_{t+1},A_{t+1}) - \alpha\log\pi_{k+1}(A_{t+1}|S_{t+1})]\\ =&\ \mathbb{E}_{\substack{S_{t+1}\sim p(\cdot|s_t,a_t)\\A_{t+1}\sim \pi_{k+1}}}[R_t - \alpha\log\pi_{k+1}(A_{t+1}|S_{t+1})]+ \gamma \mathbb{E}_{S_{t+1},A_{t+1},S_{t+2}}[R_{t+1}+\gamma V_{\pi_k(S_{t+2})}]\\ \leqslant&\ \cdots\\ =&\ \mathbb{E}_{\rho_{t+1}\sim\pi_{k+1}}\left[\sum_{i=t}^{\infty}\gamma^{i-t}(R_i-\gamma\alpha\log\pi_{k+1}(A_{i+1}|S_{i+1}))\right]\\ =&\ Q_{\pi_{k+1}}(s_t,a_t) \end{aligned}$$

由上式可知 $\pi_k$ 收敛到定义2中最优化目标的一个局部最优解

QED

---

动态调整温度系数

最后一个问题就是温度系数 $\alpha$ 的大小问题，论文$^{[1]}$中引入了一个带约束的最优化问题：

$$\begin{aligned} \max_{\pi}&\quad \ \mathbb{E}_{\rho_{pi}}\left[\sum_{t=0}^{T}R_t)\right]\\ s.t.&\quad\ \mathbb{E}_{\rho_{\pi}}[\mathcal{H}(\pi(\cdot|s_t)]\geqslant \bar{\mathcal{H}} \end{aligned}$$

其中 $\bar{\mathcal{H}}$ 表示目标信息熵（带约束的目标中要求所有 $\mathcal{H}(\pi(\cdot|s))\geqslant \bar{\mathcal{H}}$，及 $\bar{\mathcal{H}}$ 为轨迹中所有状态对应的策略的信息熵集合的下界），作者通过使用对偶问题，将 $\alpha$ 视为一个Lagrange乘子，然后将回报展开，从最终状态递归求解 $\alpha$，最后得到的结论为下式：

$$\alpha^* = \argmin_{\alpha}\mathbb{E}_{a\sim\pi^*}[-\alpha\log \pi^*(a|s;\alpha)-\alpha\bar{\mathcal{H}}) = \alpha [\mathcal{H}(\pi(\cdot|s)) - \bar{\mathcal{H}}] =: J(\alpha)$$

其中 $\pi^*(\cdot|s;\alpha)$ 表示在 $\alpha$ 给定的前提下，能够最大化奖励和带有 $\alpha$ 温度系数的熵正则项的策略，在实际算法中直接用当前的策略 $\pi$ 近似。则 $\frac{\partial J}{\partial \alpha} = \mathcal{H}(\pi(\cdot|s)) - \bar{\mathcal{H}}$，这里只能用梯度下降更新因为直接求解 $\alpha$ 要么是 $+\infty$ 或 $-\infty$。

算法实现

利用TD3中的双截断 $Q$ 值对动作价值函数进行估计，共包含五个网络

$$\pi_{\phi}(a|s),\ q_{\theta_i}(s,a),\ q_{\theta_i^-}(s,a),\quad(i=1,2),$$

其中 $q_{\theta_i^-}$ 为 $q_{\theta_i}$ 对应的目标网络。

交互和训练方法和DQN类似，首先用策略 $\pi_{\phi}(a|s)$ 和环境进行交互，并将得到的状态四元组 $(s,a,r,s')$ 存入记忆缓存当中。

然后每次从缓存中采样得到一个固定大小的batch记为 $B$，更新可分为一下三步：

1. （Critic）计算 $(s,a,r,s')$ 对应的TD目标 $\hat{y}(r,s') = r + \gamma\mathbb{E}_{a\sim\pi(\cdot|s')}\left[\min\limits_{i=1,2}q_{\theta_i^-}(s',a) - \alpha\log\pi_{\phi}(a|s')\right]$，最小化动作价值函数对应的损失，用梯度下降对参数进行更新：

$$\min_{\theta_i}\quad \mathcal{L}(\theta_i) = \frac{1}{2|B|}\sum_{(s,a,r,s')\in B}|q_{\theta_i}(s,a) - \hat{y}(r,s')|^2,\quad(i=1,2)$$

2. （Actor）最小化 $D_{KL}\left(\pi(\cdot|s)\bigg|\bigg|\frac{\exp(\frac{1}{\alpha}Q_{\pi_k}(s,\cdot))}{Z_{\pi_k}(s)}\right)$ 等价于最小化以下目标（定理4中已推导），用梯度下降对参数进行更新：

$$\min_{\phi}\quad \mathcal{L}(\phi) = \frac{1}{|B|}\sum_{(s,a,r,s')\in B}\mathbb{E}_{a\sim\pi(\cdot|s)}\left[\alpha\log\pi_{\phi}(a|s) - \min\limits_{i=1,2}q_{\theta_i}(s;a)\right]$$

3. （自动调节温度系数 $\alpha$，也可以直接固定 $\alpha=0.2$ 不自动调节）首先确定超参数目标信息熵下界 $\bar{\mathcal{H}} = -\lambda\sum\limits_{1\leqslant i\leqslant |\mathcal{A}|}\frac{1}{|\mathcal{A}|}\log\frac{1}{|\mathcal{A}|} = \lambda\log|\mathcal{A}|$ 其中 $\lambda\in(0,1)$ 为超参数。使用梯度下降对 $\alpha$ 进行更新：

$$\frac{\partial J(\alpha)}{\partial\alpha} = \frac{1}{|B|}\sum_{(s,a,r,s')\in B}\mathcal{H}(\pi(\cdot|s)) - \bar{\mathcal{H}}$$

训练效果

在KataRL中用JAX完成了SAC的实现核心代码 sac_jax.py，使用方法：

python katarl/run/sac/sac.py --train --wandb-track
python katarl/run/sac/sac.py --train --wandb-track --env-name Acrobot-v1 --flag-autotune-alpha no

训练效果可以见wandb的报告，看得出来SAC只能勉强在Cartpole-v1上和DDQN打平手，最终稳定性较优；但在Acrobot-v1上效果极差，调参也难以解决。

主要的超参数为目标信息熵大小 \bat{\mathcal{H}}，该模型对该参数的敏感度极高，或者可以不自动调整 $\alpha$，固定 $\alpha = 0.2$。